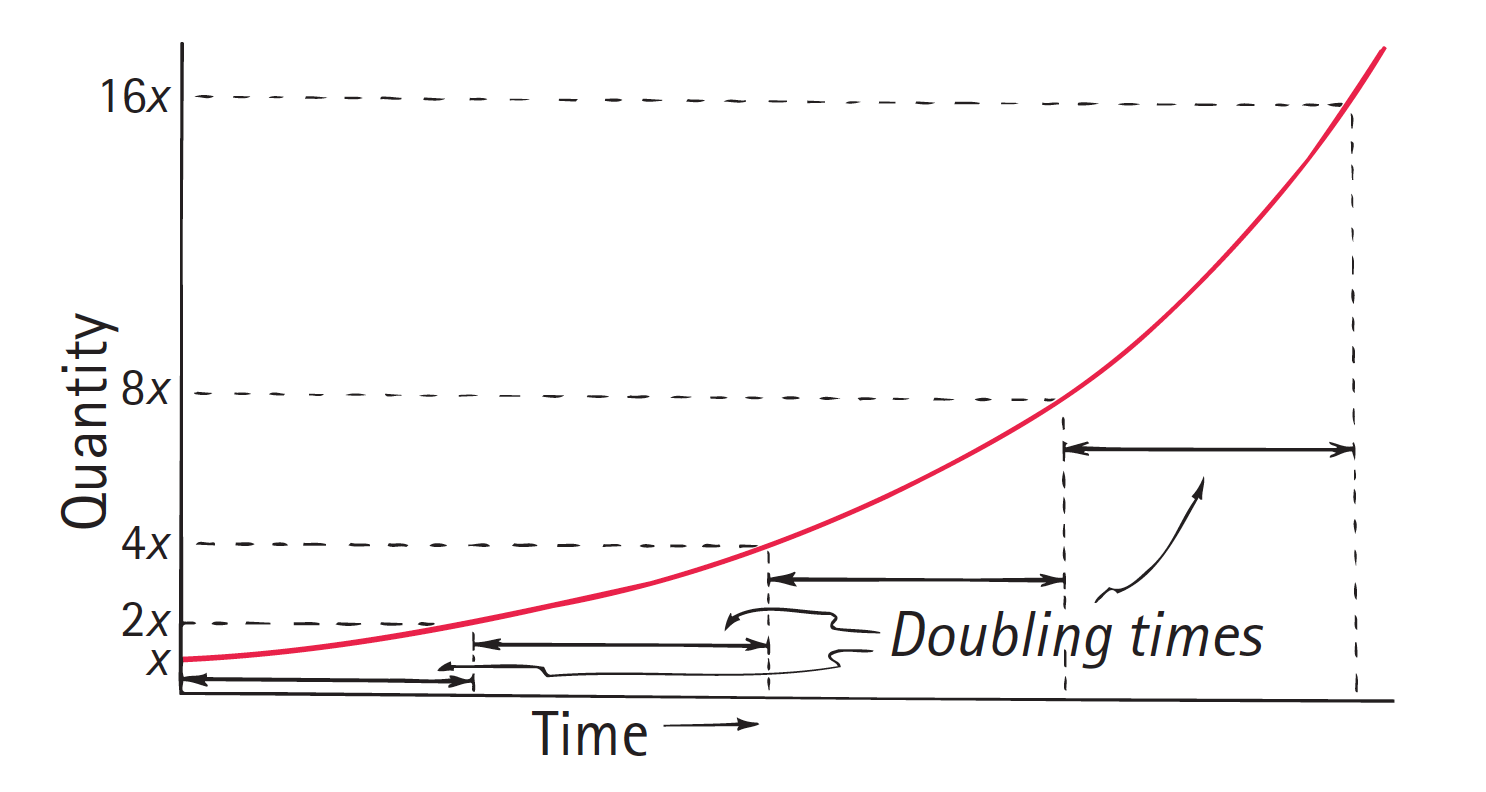
A Function Has a Constant Doubling Time

The function which has a constant halving time is in the following form Where. When x3 y doubles or y 8.

Linear Time Vs Logarithmic Time Big O Notation By Jhantelle Belleza Towards Data Science

The only non-exponential function that has this property would be a function that has the constant value of zero.

. If you dont know your growth rate you can derive it by subtracting your past quantity from your current quantity and dividing the result by. Doubling time then is the number of those periods itd take for a quantity to double. F 0 A.

Then if A is the initual cuantity. For example 70 14 years doubling time 5 or a 5 annual growth rate. For example at a 10 annual growth rate doubling time is 70 10 7 years.

Similarly to get the annual growth rate divide 70 by the doubling time. Where rate is the percentage increase you expect per period expressed as a decimal for example 5 would be 05. 3 Show answers Another question on.

To model the population at any arbitrary year we rewrite the exponential function in terms of the doubling time. We have a function of the form. But there is nothing special about halves it can also be specified by the decay constant k that appears in the exponential decay function.

Exponential growth O c. An exponential decay function represents a quantity that has a decreasing halving time. As y doubles proportionately to x.

F t A3 tT and you can see that. We can additionally expand and. The doubling time calculator has a fixed endpoint so merely enter how quickly an investment or quantity is appreciating.

1 x t x 0 b t for b 1 where x 0 is the population size at time t 0. That is y output doubles with x input y tex 2 x jd3sp4o0y and 12 more users found this answer helpful. The doubling time T double can be computed as follows for exponential growth of the form.

A₀ is the initial amount h is the half life time or the halving time. T is the time At the amount that remains at time t The previous function represents an. Depends it can be true or false Apex.

Depends it can be true or false Apex. Y ax where a is. To do this we divide 70 by the growth rate r.

For example if the population of a growing city takes 10 years to double from 100000 to 200000 inhabitants and its growth remains exponential then in the next 10 years the population will double to 400000 and. What type of function does this represent. Ft300cdot 2t12 or more generally ft300cdot 2tT where T is the doubling time.

A constant tripling time means that there is a time T a quantity triples when t T then triples again when t 2T and again when t 3T. For example a rate of 6 would be estimated by dividing 72 by 6 which would result in 12 years. The rule of 72 is found by dividing 72 by the rate of interest expressed as a whole number.

This is an exponential function. Doubling time is the amount of time it takes for a given quantity to double in size or value at a constant growth rate. Exponential decay doesnt have to have a decreasing halving time.

A function has a constant doubling time. Using the Doubling Time Calculator. An exponential decay function represents a quantity that has a constant doubling time.

What the difference between an exponential equation and a power equation. Nuclear decay is a simple random process the more of something there is the more of it will decay if the probability of decay is constant which it isthe simplest way to quantify this is halflife as you mention. The graph illustrates how exponential growth.

Decreasing linear O D. It is proved in calculus that this law requires that the quantity is given by the exponential function if we use the correct time scale. When x1 y doubles or y 2.

An important feature of exponential growth is. Also at T 70 P 02 so the population also doubled from 01 to 02 between T 48 and T 70 which is also 22 minutes. An exponential decay function represents a quantity that has a constant doubling time.

We can find the doubling time for a population undergoing exponential growth by using the Rule of 70. To calculate doubling time first multiply your growth rate by 100 to convert it to a percentage. View results An exponential function is written as Fx equals a bx where the coefficient a is a constant the base b is but not equal to 1 and the exponent x is any number.

Every twelve years the population doubles and the exponent becomes an integer based on nt12. Noting that for i 0 1 the corresponding term inside the sum would be zero we can start the sum at i 0 without affecting anything. When x2 y doubles or y 4.

C n i 2 n 1 i 2 i 1 2. Exponential decay O B. N n0 e-kt.

A function has a constant doubling time. It just decays at a certain percentage every time which might be 50 or might not. The importance of the exponential curve of Figure 1 is that the time required for the growing quantity to double in size a 100 increase is a constant.

This explains the name. As stated this is only an estimation as a 6 rate would take 1190 years using the actual doubling time formula. Making this substitution we have.

F T A3. An exponential growth function represents a quantity that has a constant doubling time. This is just i i 1 2.

What type of function does this represent.

Algorithm Constant Amortized Time Stack Overflow